A/B Testing Overview
A/B Testing is the test that we want to test for particular product. Usually A/B testing works for testing changes in elements in the web page. A/B testing framework is following sequence:
- Design a research question.
- Choose test statistics method or metrics to evaluate experiment.
- Designing the control group and experiment group.
- Analyzing results, and draw valid conclusions.
A/B testing is used to validate whether the changes that we have applied in our product is significantly affected our users instead of relying solely on the expert opinion.

Screenshot taken from Udacity 0:03
When to use A/B testing¶

A/B Testing can be used to make a convergence to global minimum, but not useful for comparing two global minimum. It also not particulary useful to make overall testing.
Consider example above:
- This example can't be used for A/B testing. It tries to answer vague question, and it's too general. We don't which specific metric/method to use to answer this. Hence the only way we can do is to test for specific product.
- It's not design to test premium service of your site. Suppose that you have a bunch of premium features and decide to do some A/B testing and divide control and experiment group. This group would not going to be roughly equal since there will be users that opt for premium, or not. And it will not affect overall users. So we could only gather knowledge, but not for full blown test.
- The third one is where A/B testing can be shine. It will affect all users, so can divide them to both groups, and we have clear metrics to test the algorithm, for example by ranking.
- The fourth one is also where A/B testing can be useful. We have all set of product that we want to test, has some metrics that we can test, as long we have both computing power.
Let's take another examples

Screenshot taken from Udacity 0:51
In the first part, we know that things like cars can be sold for a very long time. A/B testing only collect data that occurs in small window (at least for us to analyze). People comes to the website maybe 6 months to 1 year in the future to buy. And it maybe not by the website, but by other referrals. We couldn't wait that long for testing purposes, and the data won't be enough. The second part, also relates to the first reason. Updating company's logo, will take time until customer reacts. So it won't be good for A/B testing. The final part, we have clear control and experiment groups, and also clear metrics. So A/B testing does useful for this situation.
A/B testing is used as a general method online to test features, decide audience control and experiment set, and which is better. A/B testing is used to find the global maximum significant of one changes, between control group and experiment group. It doesn't too useful however to compare two changes that already at its best. Amazon personal recommendation can be increased with A/B testing, one hundres of millisecond delay at page view can be tested by A/B testing, as it always decrease 1% revenue.
A/B testing is really tricky to measure, as we need good metric to analyse. A/B testing can tell different about one changes, but not for overall changes. That's why when we usually have one big experiment, we have multiple A/B testing across multiple experiments.
Other techniques¶
Well then if we can't use A/B testing, what other techniques can be used to test changes in our product? A/B testing can be used to observe users log, make it as observational studies when the hypothesis changes, use behaviour randomized restrospective analysis. Restropective analysis give you small, but deep qualitative data, but A/B testing give you form of quantitative data.
The difference for quantitative vs qualitative is also applied when you do online vs traditional experiment. In traditional experiment, you know each of the people in your group. Not only their health status if you test new medicine for example, but also their habbit, their occupation, their family, their hobby. You know them deeply by interacting with them. But in an online experiment, all of this are gone. You only new time and possibily some ip and user agent, but that's it. You can get millions of users in an online testing, but not so deeply as small qualitative group.
History of A/B testing¶
There was no official record stated about the origin of A/B testing. But it was long applied in the aggriculture field, where farmers divide section and apply various techniques and observe which is better for distinct crop.

Screenshot taken from Udacity 1:56
We can take a web company, called Udacity for example, that want to apply changes like in the experiment in the image above stated. Usually in every digital web company, they have some funnel analysis. That is the number of users, from homepage visits, to gain actual conversion, that is final act that we actually care about. Either it's creating an account, or maybe complete a purchase. This funnel describe how number of users can be decreased down as we move to deeper layer. The idea is, if we apply this change in homepage visits, it should be increase more users to one deeper layer, 'Exploring the site'. If it's not giving significance increase, we don't want to launch it. And we absolutely don't want to launch it if the change even decrease the number of users to the next layer. Ideally if we can increase number of users to one deeper layer, then it would also have an increase to even deeper layer, that got actual conversion.
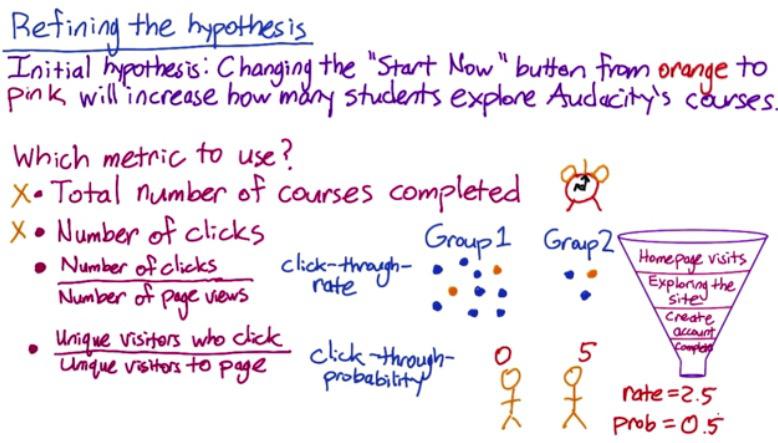
Screenshot taken from Udacity 2:19
After we have design a research question, like in the previous paragraph, we want to have test statistics that fit in our experiment. One popular alternative is CTR, click-through-rate that measures number of clicks for each particular users. But for our particular case, CTR not the best case scenario. What we actually want is CTP, click-through-probability. CTR won't give you number of unique users, it instead give number of clicks. If for example we have two person, as described above, with first person, never click, and second person have 5 clicks(probably because lagging and he's rapid clicking the button).
CTR will give you
clicks/person = 5/2 = 2.5
CTP will give you
atleastone/person = 0.5
So you see in our case, CTP is the right decision to choose, and we revise our Hypothesis with CTP as test statistics. So when do we use CTR, and when do we use CTP? CTR usually measure the visibility (button in our example), while CTP measures the impact. CTP will avoid us the problem when users click more than once. CTP can be acquired when working with engineers, to capture number of click every change, and get CTR with at least one click.

Screenshot taken from Udacity 0:22
Considering large number of samples (1000) 150 is even further, if you know about standard error.
We only have two possible possible outcome in click-through-probability, and concern probablity as metric. This would means we want to use binomial distribution, with success is the click, and failure is not click.
If you want to refresh your binomial distribution, check out my other blog.

Screenshot taken from Udacity 1:32
- dependent
- independent, 2 exclusive
- same user, same search result
- could be binomial, one event is one user complete one course. One user can't finish twice or more in one course
- can be one user multiple purchases.
Since there is two possible outcome, we would expect two peak at the distribution. When we're talking about the probability, especially with the law of large numbers, the probability becomes the proportion. p-success with click, and (1-p)-failuure with no click. Binomial require sample size that at least events occurs with click and no click are 5 times, to follow normal distribution.
If follow normal distirbution, then ME = 1.96xStandard Error.
If you need to refresh your statistics of Confidence Interval for proportion, check out my other blog.
So for example, if samples is 2000, and number of click 300, 99% confidence interval gives us....
%load_ext rpy2.ipython
%%R
c = 300
n = 2000
pe = 300/2000
CL = 0.99
SE = sqrt(pe*(1-pe)/n)
z_star = round(qnorm((1-CL)/2,lower.tail=F),digits=2)
ME = z_star * SE
c(pe-ME, pe+ME)
Now we have our CTP in the range of 95% CI (Which means that 95% CI will capture the population difference). Remember the difference is before we begin the experiment, which divide to two groups. The idea is, if we apply changes in experiment group, then the observed difference has to be significant, that it outside the range of CI. When we're talking about positive changes (in increased of CTP), then it should be outside of CI positive boundary.
Comparing two samples¶
Comparing two sample(groups) will require us to use hypothesis testing. The difference (pooled difference) should be outside CI that we talked earlier.
Again, if you want to refresh or feel alienating about estimating difference between two proportions of hypothesis testing, feel free to check my other blog.
Practical, Substantive, Significance.¶
When we're talking about difference, in statistics we know that there is practically significance and statistically significance. Statistically significance is what we calculated (our p-value). and practically significant is what we set as fixed significant level, in other words, our target leve.
Why does it matter? Because as always, gathering data is expensive, require effort, time, and investments. That's why we don't wan't waste such resources. You can see further explanation in my other blog. For business practice and investment wise, is what practical significance that matter.
So what's to decide the level of significance? For company like Google, 2% difference is quite large.
Size vs Power Trade Off¶
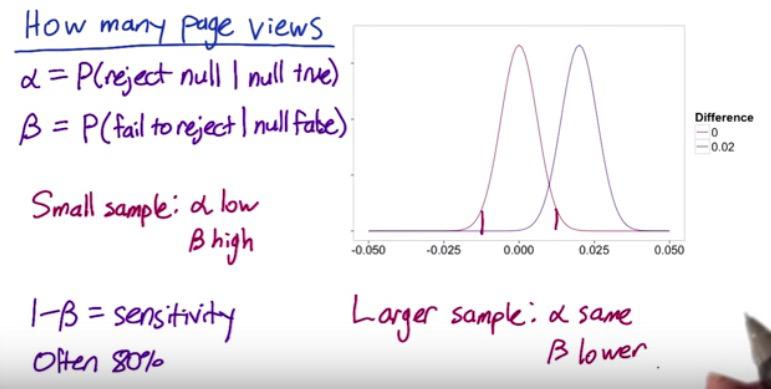
Screenshot taken from Udacity 2:40
When designing an experiment, we need to know how many pageviews (size of the data) to find what's statiscally significance/ statistics power.
In Hypothesis testing, we can't blindly reject null hypothesis, when the statistics is only slightly lower than practical significance.
There are trade-off that we know here. Increasing the size of the data will cost some investments. But it also making it more sensitive to the changes. And if it does make positive difference, then it will be profit for the company. This is what earlier we call statistical power, the sensitivity. (1-B) is the probability of correctly rejecting null hypothesis, which in this case we set it to 80%. (1-B) depends on the size, larger would means distance different is further between point estimate and null value. B is the subject of type 2 error.
We set alpha as our difference at practical significance, and beta is the sensitivity, which control the failure on what we actually care about. We want beta to be inside alpha range (practical significance boundary, later at CI), by 80%. If we have small size of data, then type 2 error will be high, too high that it's within CI range, and we failed to reject null hypothesis. On the contrary, larger sample means, will makes alpha(as practical significance) still the same. Remember that larger sample means will raise the sensitivity, makes the standard error smaller and the CI range will be tighthen, too tight that can makes beta outside CI range
If you want to see further about Type 1 error, Type 2 Error, Beta, and power, please check this blog
Calculating number of page views needed¶
How many pages will we need in each group?
If we look at our problem earlier, Suppose we have:
N = 1000
x = 100
alpha = 0.05
Beta = 0.3
dmin = 2% (practical significance level)dmin = minimum difference that we actually care about, with business practive

Screenshot taken from Udacity 2:40
Remember the sample size smaller, means higher standard error. If we increase the sample size, by the law of large numbers, it will approach closer to equal proportion, and further away from extreme.
If we increased our dmin, then it would means we have more loosely significance. That we would accept if the difference is small, 20% dmin will have more error than 5% dmin. An increase in error, can be caused by decreasing the sample size.
Increasing CI would increase the sample size. 95% level is a smaller range compared to 99% range, which means if we use 99%, the difference have to even further away to be outside the boundary range. And making the distance really different between null value and point estimate require larger sample size.
Higher sensitivity, as we discussed earlier, will narrow the error distribution, hence require larger sample size.
Analyze¶

Screenshot taken from Udacity 0:55
Suppose we have our proportion of users based on number of click and number of unique users. Not equally same size because random assignment.
There are two factors to consider when deciding the result of your A/B testing, that is whether to launch the change or not. First one is statistically significance must be different from zero. And the change is greater than your preference practical significance boundary.
CI Breakdown¶
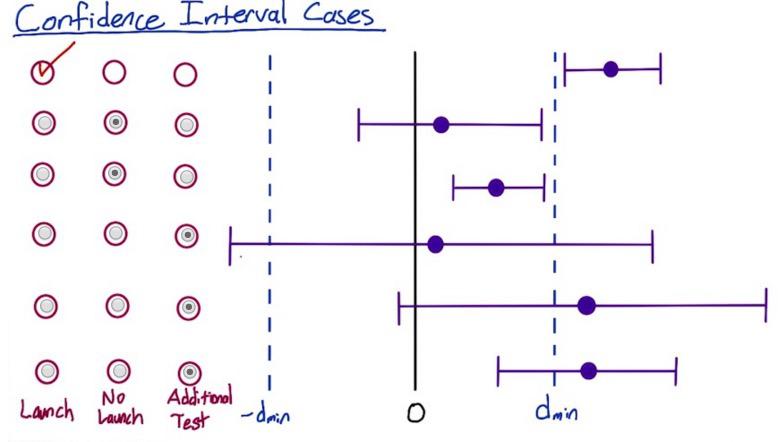
Screenshot taken from Udacity 02:05
There are various cases where our CI could have positioned in difference range of the boundary. So it's best to get intuition behind it.If your confidence interval can capture the practical significance boundary, then it might be better to run some additional test. The first one is where we absolutely launch in the previous example. Because it's outside practical significance boundary.
The second and the third one is not even touching the boundary, and because it's still within, it's not significance hence we not launch it.
The next three intervals is trickier. They all touch the boundary. the longest CI touch both lower and upper boundary. If it outside lower boundary, we definitely not want to launch it, but nonetheless the other side touch the upper boundary. So we want to perform additional test. And the last two, the proportion is centered outside upper boundary, but their lower interval still within practical significance. So we want to proceed to additional test.
Doing some additional test for the last 3 CI is needed as repetitive test gives us confidence. But it will require more sample and time, investment that some of the business side in your company wouldn't do. It's best to discuss with them further, along with additional risk if they insist to launch the changes. They know better from our recommendation, along with business strategy.
Disclaimer:
This blog is originally created as an online personal notebook, and the materials are not mine. Take the material as is. If you like this blog and or you think any of the material is a bit misleading and want to learn more, please visit the original sources at reference link below.
References:
- Diane Tang and Carrie Grimes. Udacity